

This equation holds true for −50, then shouldn't x be smaller than -5 and greater than 3? I know that doesn't satisfy the equation given in the question but I was wondering how this was possible if the sign ">" meant that the solution lies on the left of the smaller root and on the right of the bigger root. Given that xx is an integer from -10 and 10, inclusive (21 values) we need to find the probability that −x^2−2x+15 is greater than zero, so the probability that −x^2−2x+15>0įactorize: (x+5)(3−x)>0. Re-arrange the given equation: −x^2−2x+15=m If x^2 + 2x -15 = -m, where x is an integer from -10 and 10, inclusive, what is the probability that m is greater than zero? So in this post, it says that if the sign is "", then x lies on the left of the smaller root and on the right of the bigger root. However I'm a little confused, it'll be great if you can help me out here. I read this post of yours and it was extremely helpful. For example: \(-x^2-x+12>0\), first rewrite this as \(x^2+x-12 below ( "0\), then the answer would be \(x3\) (to the left of the smaller root and to the right of the bigger root). This approach works for any quadratic inequality. Then check each interval whether or not the function is. Answer is \(x3\) (to the left of the smaller root and to the right of the bigger root). Solving a quadratic inequality without a y term requires finding the zeroes and using those zeroes to determine up to three intervals. ">" sign means in which range of \(x\) the graph is above x-axis. 3) Test a number from each region formed by the. 2) Place these numbers on the number line. Before we start, let us recall that the standard form of a quadratic equation is ax2 + bx + c 0. Solving Quadratic Inequalities 1) Solve associated equation. Once mastered, this concept can be used for any inequality involving polynomials and makes solving a complex inequality question, a mere walk in the park.
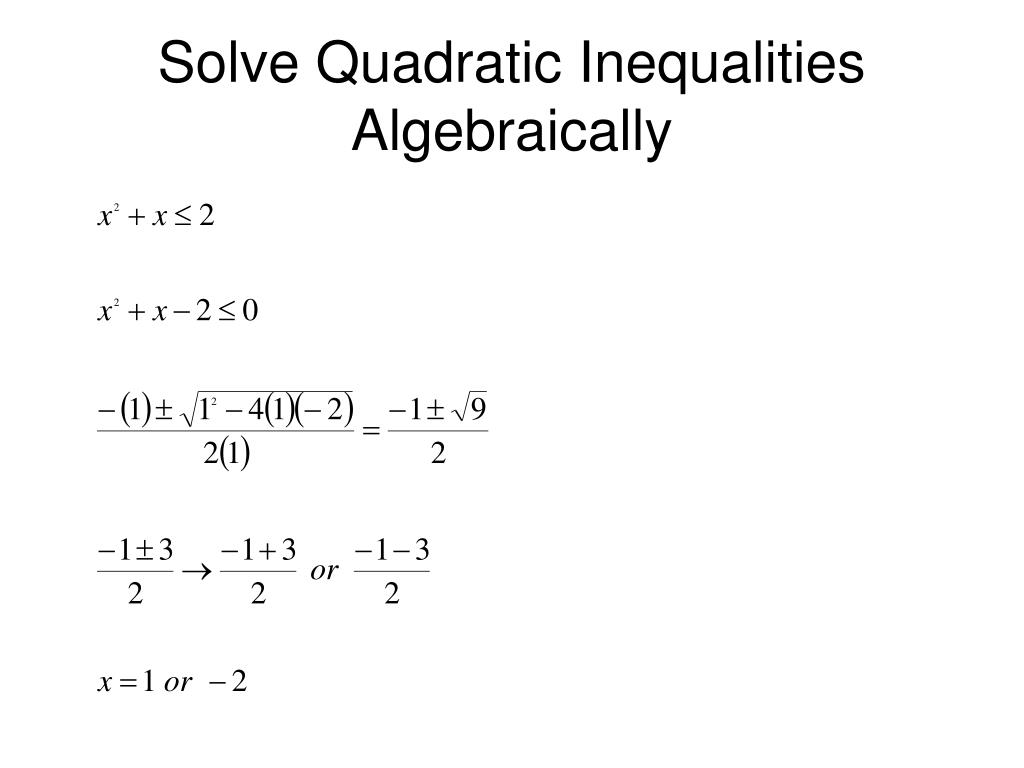
First find the roots (\(x_1=1\) and \(x_2=3\)). Quadratic inequalities are an important and often overlooked concept on the GMAT. Solving Quadratic Inequalities: Graphic Approach "img": "/forum/images/mba_dashboard/image_5.png",
#Solving quadratic inequalities free
"helpContent": " Sign up for AdCom Q&A \n \n\n\n - Tue Oct 18\n\n\n - Wed Oct 19\n\n\n \n Links:\n - 1,000+ App Fee Waivers\n- Free GMAT Club Tests\n - E-mail support\n\n ", "default_html": "\n Learn More | Register"

"default_html": "\n\n Learn More | Register \n" "Hiding it while no sessions are taking place", "name": "Unveiling 13-week Ultimate Study plan by GMAT Ninja", "name": "6-Week Plan for creating an Impressive R2 App", "name": "What matters most in your MBA App by ApplicantLab", See the Inequalities Calculators by iCalculator™ below."regUrl": "/forum/redirect.php?id=nxcyfldet4",
#Solving quadratic inequalities full
Check your calculations for Inequalities questions with our excellent Inequalities calculators which contain full equations and calculations clearly displayed line by line.Test and improve your knowledge of Quadratic Inequalities with example questins and answers


 0 kommentar(er)
0 kommentar(er)
